Ancient Chinese Zero as a Place Holder

The Chinese used a counting board to do their math, and an additive system to write their numbers.  There was a symbol for 1 and a symbol for five and these symbols were added together to form symbols for other numbers up to 9. The numbers were actually rods arranged on a counting board which ran from left to right.  Any missing places were left blank on the counting board.

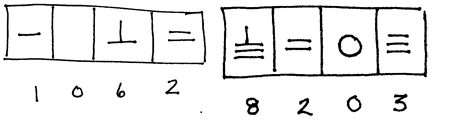
Ancient Indian Zero as a Place Holder

Modern positional notation, where each digit has a varying value depending upon its position in the representation of number, is simply the notation of the counting board made permanent.  All that is needed to transfer a number from the board to paper is ten different symbols; one, two three, four, five, six, seven, eight, or nine beads, or no beads at all.  The column can be empty, and the tenth symbol must of necessity be a symbol for such an empty column.  Otherwise, it would be impossible to distinguish among the different numbers from the counting board.

Without such symbol, the above example would all on paper be the same: 234.  With a symbol, they are easily distinguishable as 2,340, 2,034, 2,304.

It would seem that the first time anyone wanted to record a number obtained on a counting board, he would automatically must put down a symbol of some sort –a dash, a dot, or a circle –for that empty column, which we today represent by zero (0): 

But, in the thousands of years, nobody did. 

Sometimes in early century of the Christian Era, an unknown Hindu who wanted in permanent form the answer on his counting board, put down a symbol of his own invention, a dot, he called sunya, to indicate a column in which there were no rods or no beads.   The earliest use of a vocabulary of symbolic words to note zero is known from the 458 AD cosmology text Lokavibhaga.

It has been pointed out by some that the invention of a symbol for nothing, the void, was one for which his philosophy and religion had peculiarly prepared the Hindu.  But, it must be understood that dot sunya which the Hindu created was not the number zero.  I was merely a mechanical device to indicate an empty space and that was that the word itself meant --empty.  The Indians still use the same word and symbol for the unknown in an equation --what we usually refer as x --the reason being that until a space is filled with a proper number, it is considered empty. 

With sunya, the symbol zero had been invented; but the number zero was yet to be discovered. 

Modern Zero as a Decimal Number

The historian Will Durant wrote:

<<

In 773, at al-Mansur's behest, translations were made of the Siddhantas Indian astronomical treatises dating as far back as 425 B.C.; these versions may have been the vehicle through which the "Arabic" numerals and the zero were brought from India into Islam.  In 813 al-Khwarizmi used the Hindu numerals in his astronomical tables; about 825 he issued a treatise known in its Latin form as Algoritmi de numero Indorum  -- "Al-Khwarizmi on the Numerals of the Indians"; in time algorithm or algorism came to mean any arithmetical system based on the decimal notation.  In 976 Muhammad ibn Ahmad, in his Keys of the Sciences, remarked that if, in a calculation, no number appears in the place of tens, a little circle should be used “to keep the rows.”

 >>

~(‘The Story of Civilization’, Volume  4, 'The Age of Faith' pp. 241)

This is the first time that zero was put in writing on a piece of paper. 

Transmission to Europe

The Hindu–Arabic numeral system (base 10) reached Europe in the 11th century, via the Iberian Peninsula through Spanish Muslims, the Moors, together with knowledge of astronomy and instruments like the astrolabe, first imported by Gerbert of Aurillac. For this reason, the numerals came to be known in Europe as "Arabic numerals". The Italian mathematician Fibonacci or Leonardo of Pisa was instrumental in bringing the system into European mathematics in 1202.

In Europe, the number 10 was X and the number 20 was XX, etc. They only knew numbers in that way. Muslims were the first to use zero as a space holder in decimals like 10, 100, 1000, etc.

Then the Muslims brought this gift of zero and Algebra to the Europeans in or around 1500. Afterwards, one European, named Boolean, enhanced the Algebra with Boolean Algebra. Boolean Algebra is the calculation of numbers with zeros and ones.

Fast forward, now, we have computers. Computers communicate with zeros and ones (0101001). Zero means the light is off and 1 means the light is on. When I push "A", my computer turns the light on and off 10 times and sends this as a digital signal to your computer.

Zero and Computers

Computers communicate with each other with lights (Fiber Optics) or Electrical Signals. The advantage of using light is you can beam it through satellites, just as you would beam light through mirrors. When you see lights turning on and off very quickly in a network, it means there is a network communication of different computers. This OFF and ON is represented by 0s and 1s, respectively. Calculating with 0s and 1s is called [[Boolean algebra]]. In a computer, ON means 1 and OFF means 0. One English alphabet is represented by a bunch of binary numbers. For example, A=01000001, B=01000010, C=01000011 etc. etc. So, when you push the alphabet “A” on the computer, there is a cut off time, and this is “01000001”.  One computer sends this binary number (“01000001”) and the receiving computer interprets it to “A”. Each color has its own binary numbers. That is what it means when we say that a camera is a digital camera --it simply means, it understands binary numbers. However, since we cannot write with binary numbers, we must use computer languages to write the binary numbers in the computers for us. The computer languages in turn work between the users and the computers. In other words, as you are reading this, behind this page, there is a computer language page; behind that computer language page, there is a binary number language page; behind that binary number language, there is 0s and 1s page; and behind 0s and 1s, there is light on and off page.

More info:

For the early Chinese math and history of zero, read:

www.mediatinker.com/blog/archives/008821.html

For more readings, see, From Zero to Infinity: What Makes Numbers Int…(Paperback) by Constance Reid

http://www.historyofscience.com/G2I/timeline/index.php?category=Mathematics+%2F+Logic